Information Entropy : TLDR

An introduction to a few big ideas in information theory including

  • information entropy
  • thermodynamic entropy
  • Huffman codes

Jim Mahoney | Dec 2019

By Jacobs, Konrad - https://opc.mfo.de/detail?photo_id=3807, CC BY-SA 2.0 de, https://commons.wikimedia.org/w/index.php?curid=45380422

Claude Shannon

He defined "information entropy" as

$$ S = \sum_i p_i \log 1/p_i $$

in units are "bits of information per bit".

What the heck is all that? Well, I'm glad you asked.

What is "information"?

Suppose I send you a sequence of symbols, and you try to guess the next one in the sequence.

Here are some examples.

  • A : 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, ?
  • B : 1, 1, 1, 1, 1, 1, 1, ,1, 1, 1, 1, 1, 1, 1, 1, 1, 1, ?
  • C : 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, ?
  • E : o n e _ t w ?

Shannon's idea was that the easier it is to guess the symbol, then the less information that symbol conveys.

In other words, how surprised you are by a symbol is how much information it has.

Extreme cases

completely random : 0, 0, 1, 0, 1, 1, 0, 1, 0, ...

  • P(1) = 1/2 , P(0) = 1/2
  • S = 1 bit of information per 1 bit sent

completely predictable : 1, 1, 1, 1, 1, 1, , ...

  • P(1) = 1 , P(0) = 0 (for example)
  • S = 0 bits of information per 1 bit sent

(Why are we talking about probability all of a sudden?)

Two bits per symbol ...

Suppose the sequence is made up of pairs of bits, (0,0) or (1, 1) each with 50/50 chance?

  • 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, ...
  • 1st bit of pair has S = 1
  • 2nd bit of pair has S = 0
  • altogether ?

(Would you ever want to send a sequence like this?)

Aside : entropy in physics

  • $\Omega$ : number of states
  • i.e. how many ways a system can rearrange its micro-stuff without changing its macro properties
  • ... quantum mechanics !

Entropy explains why systems move towards an equilibrium, from less likely to more likely

BEFORE : less likely (as we'll see in a minute)

AFTER : more likely

before

If the stuff on the left stays on the left, and the stuff on the right stays on the right, then ...

  • $\Omega_{left} = 4$
  • $\Omega_{right} = 4$
  • $\Omega_{total} = 4 * 4 = 16 $

after

  • $\Omega_{left} = 6 $
  • $\Omega_{right} = 6 $
  • $\Omega_{total} = \Omega_{left} * \Omega_{right} = 36 $

If all the configurations of circles are equally likely, then they are more likely to be spread evenly between the two sides.

Combining amounts with multiplication??

But if we want to think of $\Omega$ as a physical property, we have a problem.

  • If one thing has mass 10 and another mass 20, then the total is 10 + 20 = 30
  • If one volume is 7 and other is 8, then the total volume is 7 + 8 = 15.

We never find a combined total amount by multiplying amounts for each piece.

So ... use a logarhythm to turn multiplication into addition. 🤨

Entropy is not $\Omega$ but $ \log(\Omega) $ .

By Daderot at English Wikipedia - Own work, CC BY-SA 3.0, https://commons.wikim\edia.org/w/index.php?curid=507663

Boltzmann

The guy who invented the statistical version of entropy is Ludwif Boltzmann, who even wanted the definition carved on his tombstone.

$$ S = k_B \ln \Omega $$

Let's look a little closer at this log stuff.

logs !

  • The log of a number is its exponent : $ \log_{10} 100 = 2 $
  • $ 10 * 100 = 1000 $
  • $ 10^1 * 10^2 = 10^3 $ ... exponents add !
  • $ (\log 10) + (\log 100) = (\log 1000) $

  • $\Omega_{left} = 4$
  • $\Omega_{right} = 4$
  • $\Omega_{total} = \Omega_{left} * \Omega_{right} = 16 $ ... number of statues multiply

So ...

  • $ \log_2 \Omega_{left} = 2 $
  • $ \log_2 \Omega_{right} = 2$
  • $ \log_2 \Omega_{total} = \log \Omega_{left} + \Omega_{right} = 4 $ ... but their logs add!

back to probability

For each of those conceptual marbles, we turn the physics notion of "which state is this in" into the information theory idea of "which symbol are we getting now".

So we turn the number of states into a probability.

Consider $\Omega = 4$ for the picture with one of those balls in one of four states.

The probability of finding it in a one of those four is $ p = 1/4$ .

$$ \log \Omega = \log \frac{1}{p} $$

... which is almost Shannon's information entropy formula.

per symbol

The last step in connecting physics entropy to information entropy is to see that the physics entropy is defined for the whole system, while Shannon's information entropy is defined per symbol in the sequence.

So if we have many symbols $i$ with different probabilities $p_i$, each with an entropy $\log 1/p_i$, the last step is to just average them to get

information entropy

$$ S = \sum_i p_i \log 1/p_i $$

Wait, that was an average !?

Yes, for any $f(x)$, the average of f(x) is $\sum p(x) f(x)$.

To see this, lets take the average of these numbers.

$$ (1, 1, 1, 5, 5, 10) $$

The average is often written as

$$ \frac{ 1 + 1 + 1 + 5 + 5 + 10 }{6} $$

But that can also be written in terms of how many of each we have

$$ \frac{3 * 1 + 2 * 5 + 1 * 10}{6} = \frac{3}{6} * 1 + \frac{2}{6} * 5 + \frac{1}{6} * 10 $$

Or in other words,

$$ \text{average}(x) = \sum p(x) * x $$

where $p(x)$ is the probability of x.

Back to bits

For binary data of 0's and 1's, if each bit arriving doesn't depend on the previous ones, then our model of the data is just the probability of each. If we let $P_0$ = (probability of 0), then

$$ P_0 + P_1 = 1 $$

Our formula for information entropy is then just

$$ S = P_0 * \log2 \frac{1}{P_0} + P_1 * \log2 \frac{1}{P_1} $$

or

$$ S = P_0 * \log2 \frac{1}{P_0} + (1 - P_0) * \log2 \frac{1}{ 1 - P_0 } $$

And this is something we can plot.

The entropy is highest at "1 bit of information per 1 bit of data" at $P_0 = P_1 = 0.5$ . Anything else has less information per bit.

In [32]:
plot_entropy()  # .. and who doesn't like plots in xkcd style?

Let's see some code!

OK, time for a somewhat more realistic example.

This week I've been reading "The Wandering Inn" (wanderinginn.com). Here's the first paragraph.

The inn was dark and empty. It stood, silent, 
on the grassy hilltop, the ruins of other structures 
around it. Rot and age had brought low other buildings; 
the weather and wildlife had reduced stone foundations 
to rubble and stout wooden walls to a few rotten pieces 
of timber mixed with the ground. But the inn still stood.

Can we find the information entropy of that? And what will that mean?

In [12]:
# Using just the probabilities of individual characters, 
# without looking for longer patterns the analysis looks like this.
text = 'The inn was dark and empty. It stood, silent, ' + \
       'on the grassy hilltop, the ruins of other structures ' + \
       'around it. Rot and age had brought low other buildings; ' + \
       'the weather and wildlife had reduced stone foundations ' + \
       'to rubble and stout wooden walls to a few rotten pieces ' + \
       'of timber mixed with the ground. But the inn still stood.'

count = {}                   # {character: count} i.e. {'T':34, ...}
for character in text:
    count[character] = 1 + count.get(character, 0)
    
n_characters = sum(list(count.values()))

probability = {}             # {character: probability} i.e. {'T': 0.04, ...}
for character in count:
    probability[character] = count[character] / n_characters
    
entropy = 0
for p in probability.values():
    entropy += p * log2(1/p)         # information entropy formula !
print('entropy is ', entropy)

entropy is  4.166746762972305

And so?

  • What does an entropy of 4.2 bits of information per symbol mean?
  • Well, characters are typically stored in ASCII i.e. 8 bits each.
  • ... but it looks like we don't need that many bits for files like this.
  • This tells us how much that file might possibly be compressed (from 8 to 4.2)
  • ... without losing any of its information.
  • And since our probability model is simplistic here - only looking at one letter at a time - more compression is likely possible.

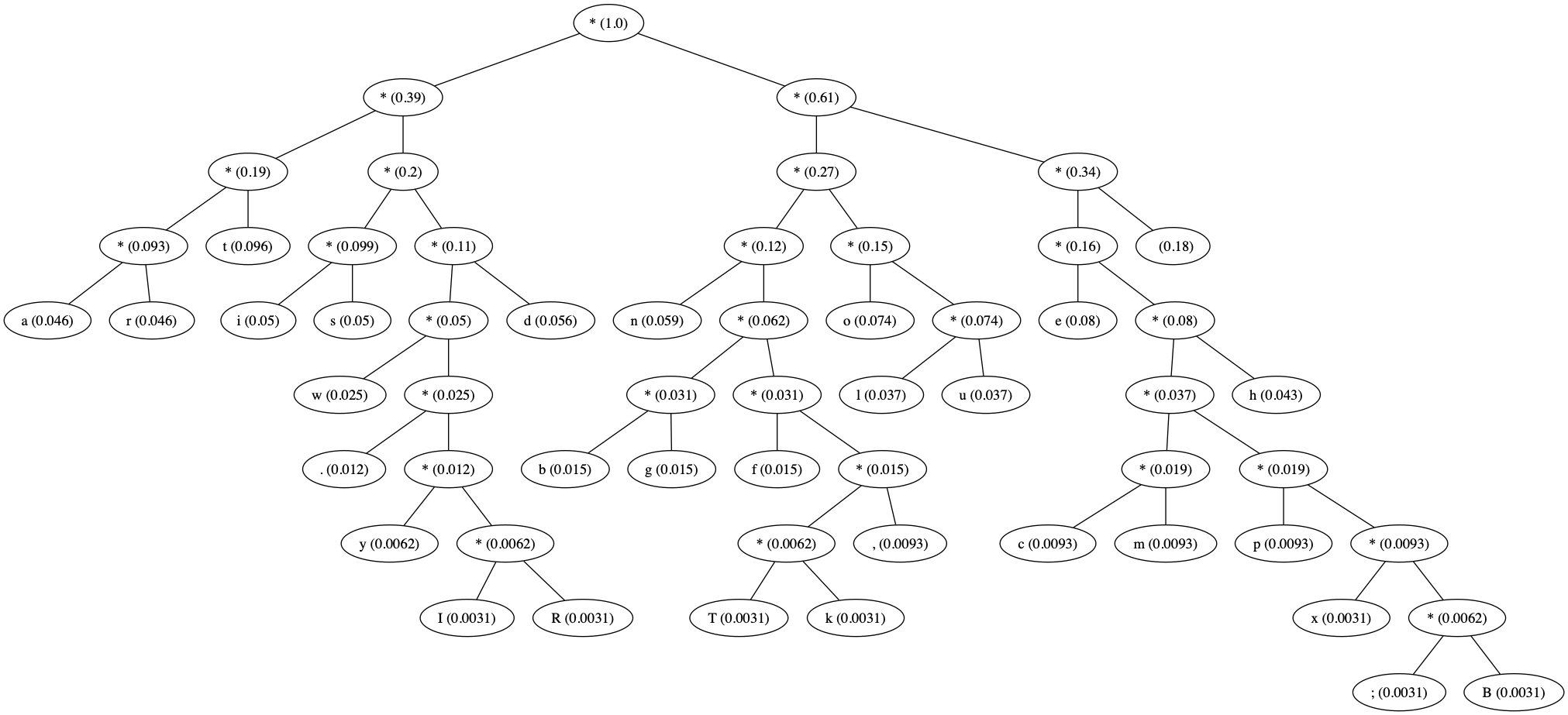
Huffman code

  • But how can we actually accomplish that compression?
  • One way is to use something like Morse code.
  • The idea is to have fewer bits for most likely characters.

Turns out there's a clever way to construct such a scheme:

  1. sort symbols by probability, low to high
  2. build a binary tree by combining the probability of the two lowest
  3. read off the codes as left=0, right=1, top to bottom

This scheme gives us a code which has the property that no character is the start of some other character, which means we don't need anything extra to tell characters apart.

Huffman example

Suppose we have four symbols (00, 01, 10, 11) with probabilities (0.6, 0.2, 0.1, 0.1).

symbol    code

00        1
01        01
11        001
10        0000

Huffman for Wandering Inn ?

wandering inn huffman tree

What comes next ?

This is the start of information theory, but of course there's still lots more good stuff :

  • more sophisticated probability models (i.e. better ways guess what's coming)
  • more lossless compression algorithms (LZW, BZIP, ...)
  • lossy (i.e. lose info) compression for images, sound, video (jpeg, ogg, mp3, ...)
  • error correcting codes : add redundancy so that noise & bit errors can be undone

In conclusion

  • "information entropy" is a profound and useful concept
  • intimately connected to randomness
  • analogous to physics entropy

Questions?