
We now turn to decisions - how to let your program do different things depending on what its variables are.
Here's an example
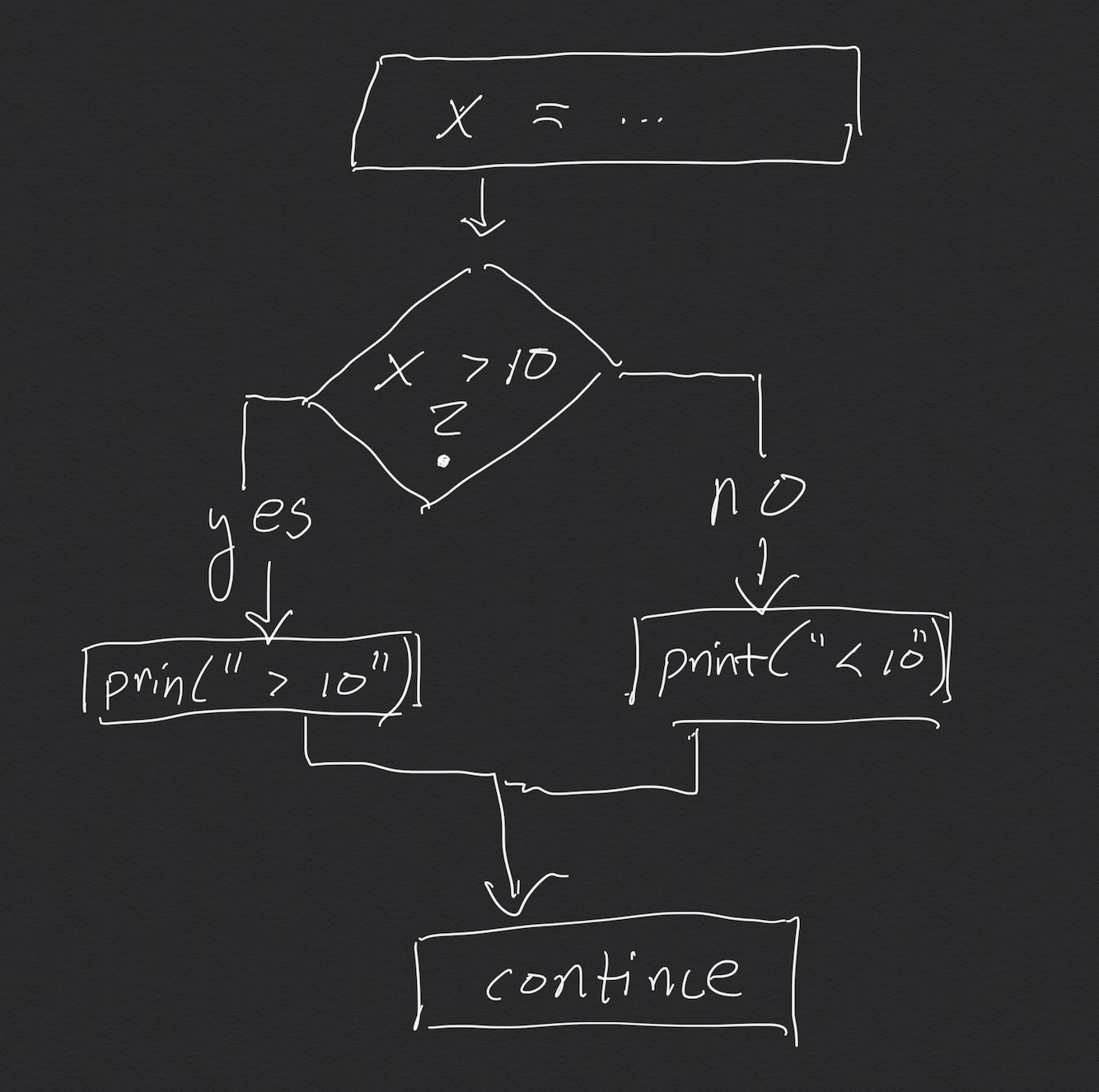
x = eval(input("Please type a number. "))
if x > 10:
print("Your number is bigger than 10.")
else:
print("Your number is 10 or smaller.")
print("... continuing")
Try that in pythontutor.com to see what happens (copy that code, and paste it in) and in particular which statements get run when you put in different values for x.
Only one of the two indented blocks will be run, depending on the value of x.
This situation can be visualized as a fork in the road, where the program executation takes one path or another.
A diagram called a "flowchart" is one way to try to visualize this.
We haven't used flowcharts before, but we could have.
Here's a program with a simple flowchart - just one line run after the other.
x = 3
y = 3*x
print(f"Three times {x} is {y}")
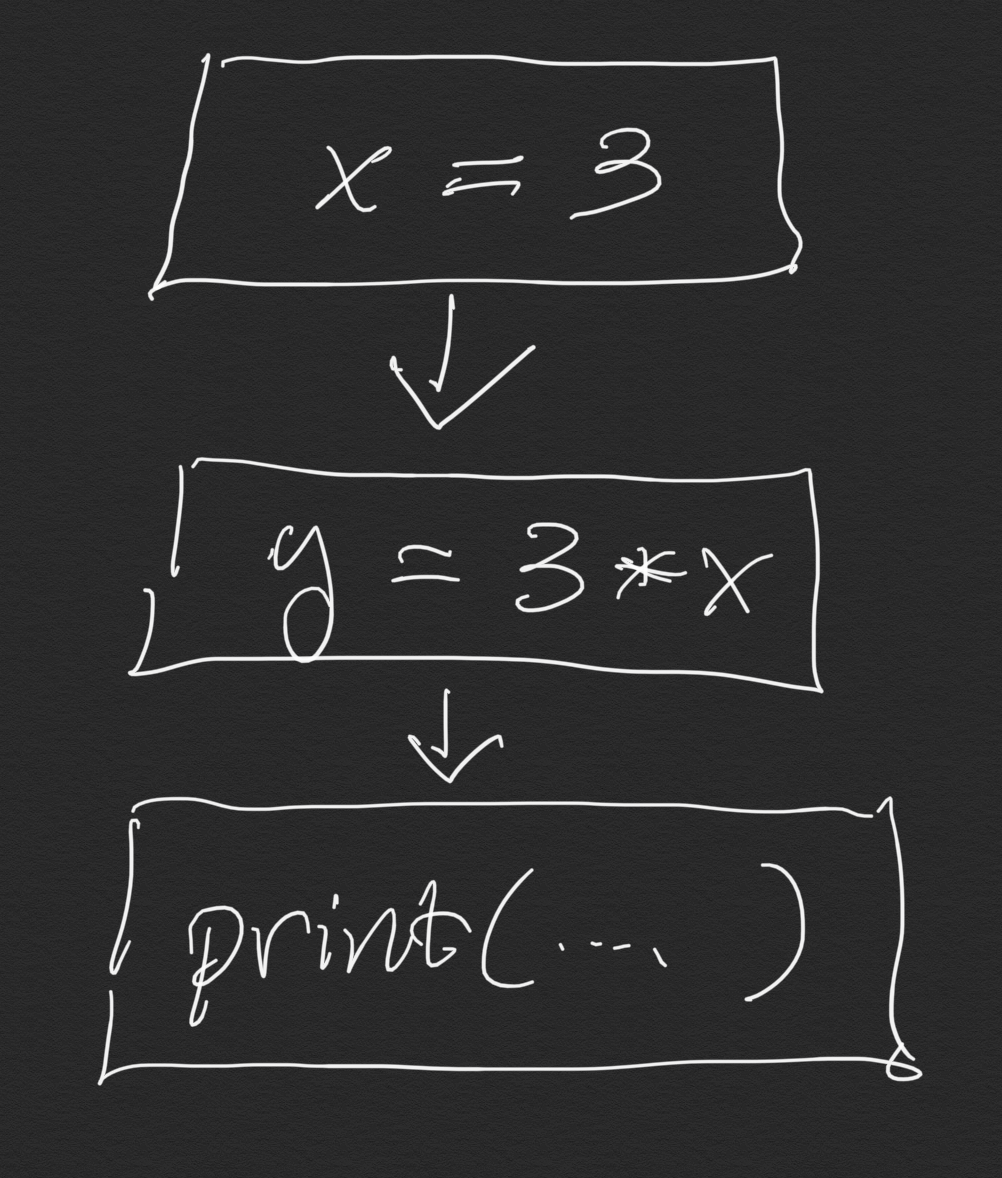
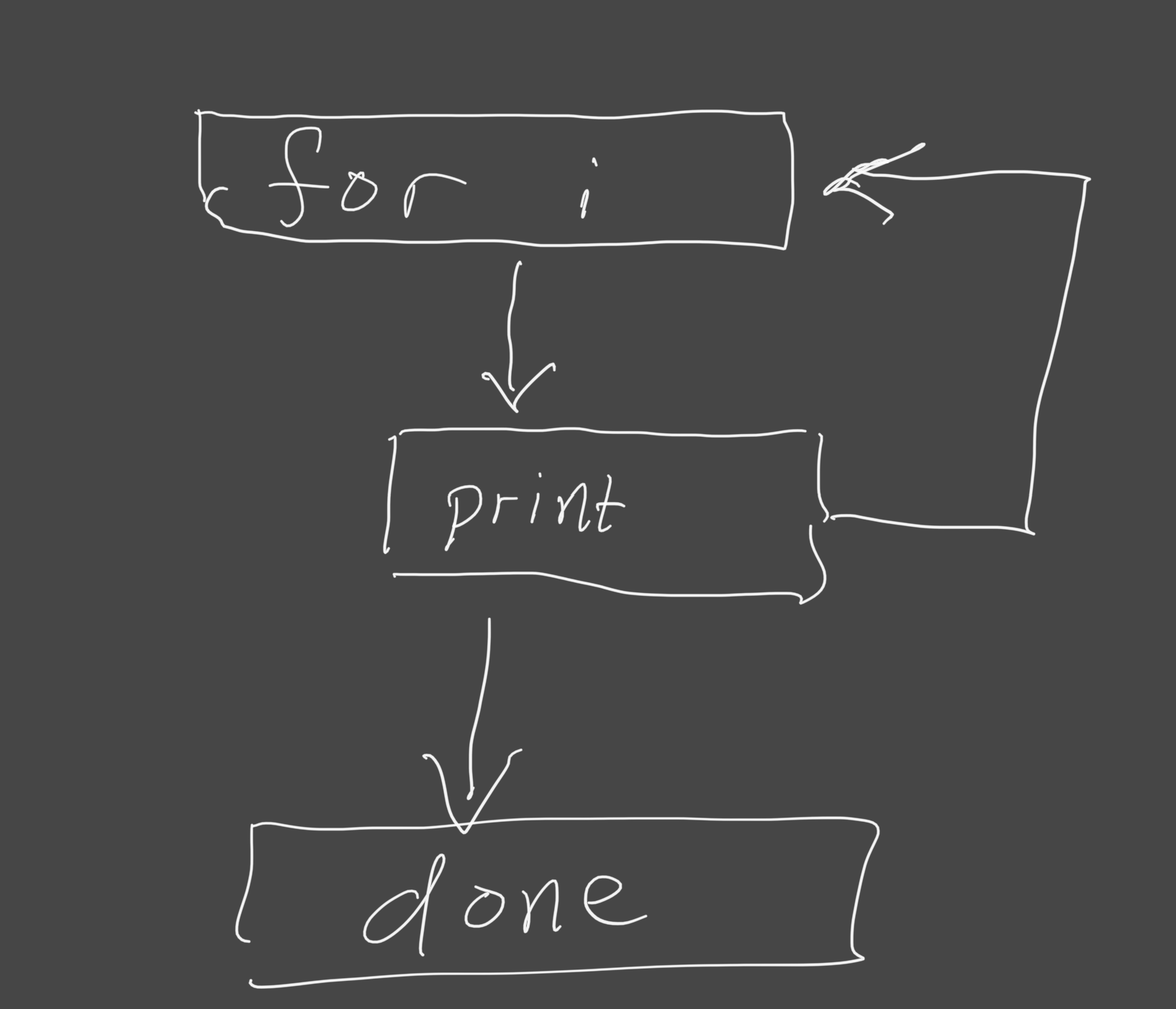
We've also done loops, which in a flowchart representation has an arrow returning to a previous line, like this.
Now we have something new: "if" statements, which ask a question, and go in different directions depending on the answer.
There is even an xkcd flowchart which explains flowcharts.
The material in chapter 7 of the textbook walks you through an example of if statements within if statements, working through how to make several choices in a row to find the maxiumum of several variables.
One python peculiarity worth mentioning: it's not uncommon to put several "if ... else" options in a sequence. For example, if you want to test to see if a word is "cat" or "dog" or "monkey" and do something different for each, then you could think of it like this :
if word == 'cat':
print("word is cat")
else:
if word == 'dog':
print("word is dog")
else:
if word == "monkey":
print("word is monkey")
That works, but the indentation gets out of hand quickly, and it's hard to easily see the alternatives.
Instead, python has an "else if" construct which collapses the "else: if ..." into one line. However, python being python, the author decided to spell "else if" as "elif". Like this :
if word == 'cat':
print("word is cat")
elif word == 'dog':
print("word is dog")
elif word == "monkey":
print("word is monkey")
The determining factor for these decisions is a new type
of python data, called a "boolean". This is just a fancy
math word for "true or false". In fact, python has
these concepts as built-in values, in the same way that
numbers are built-in. They are spelled True and False
in python. (Other languages have other conventions.)
>>> type(1) # an integer constant
<class 'int'>
>>> type("hello") # a string constant
<class 'str'>
>>> type(True) # a boolean constant
<class 'bool'>
There are lots of possible strings and numbers. But there are only two boolean values ... either True or False.
We have already seen the + operator. It takes two numbers,
and returns a number. So for example 2 + 3 turns into 5.
Now we will look at some new comparison operators: (< > <= >= ==). Each of these compares something on its left with something on its right and gives back a boolean answer, either True or False. I think it's helpful to think of these operators as asking a question, and so in the table I've put a question mark in the description.
Here's a table of some boolean operators.
operator description
------- -----------
< less than?
> greater than?
<= less than or equal to?
>= greater than or equal to?
== equal?
And here's some python code as an illustration
x = eval(input("Type a number. "))
if x == 10: # is x 10 ?
print("x is 10.")
if x < 10:
print("x is smaller than 10").
if x > 10:
print("x is bigger than 10").
if x <= 10:
print("x is less than or the same as 10").
if x >= 10:
print("x is bigger or the same as 10")
Copy that into pythtutor.com and try it out.
The comparisons are valid python expressions on their own, without the "if". Each is a True or False value.
$ python
>>> x = 10 # put 10 into x : an assignment statement
>>> 10 == x # as a question: is 10 equal to x ?
True
>>> x == 11 # is x equal to 11?
False
>>> x < 100 # is x less than 100
True
>>> answer = x < 5 # put False into answer
>>> print(answer)
False
We have already seen numeric operators which combine numbers to give another number.
operator description example result
-------- ----------- ------- ------
+ add 2 + 3 5
* multiply 2 * 3 10
So too booleans have their own operations,
ways to combine boolean expressions to
give a boolean result, for example x > 10 and x < 20.
Here's a table of some of these operators.
operator description example result
------- ----------- --------------- ------
and both true? 8 > 1 and 8 > 9 False
or one true? 8 > 1 or 8 > 9 True
not negate not 1 == 2 True
All of this is part of mathematical logic, a deep rabbit hole that we don't need to master completely now. But you should understand at least the basics as given above.

One fun example of this sort of math is Lewis Carroll's Puzzles . From that article :
"Carroll is best known for his nonsensical
books, including the infamous 'Alice in Wonderland',
written for children of ages five to ninety; but
his main line of work was as a professor of mathematics
at Oxford University in England. He studied logic as a
vocation, and he played with logic in his writings."
Logic and boolean algebra is also the foundation of computer chips themselves. We can think of the (0,1) bits in a computer as tiny little (False,True) values, and therefore the ways that we can combine them are just the logical operations. Computer chips are made up of "logic gates"; microscopic semiconductor parts that act like logic operators. Tiny wires can carry a high voltage for a 1, a low voltage for a 0, and "logic gates" can implement operations like (AND, OR, NOT). See for example the logic gate wikipedia article for more background.
But all of that is outside the scope of what we're doing here. Maybe sometime in the future I'll do a NAND to Tetris course that uses those ideas to simulate a computer from the bottom up, to understand how it works.
Besides the "for" loops that we've already seen, python also has "while" loops, which don't require a specific sequence of values but instead loop until a condition is met. "while" loops are more general than "for" loops.
Here's a simple example.
x = 0
while x < 10:
print('x is ', x)
x = x + 1
print('Done.')
Each time the "while" line is run, the boolean condition is evaluated. If it's True, then the indented block is run. If it's False, then the next line to run is the one after the indentation.
Our textbook describes several variations of the while loop in chapter 8.
Python also has ways to jump to the next loop iteration or out of a loop completely; see the flow control docs for the details.
And you can also jump out of a loop
and its enclosing function a return statement.
For example, here's a function that returns
how many guesses it took for the user
to guess a number. The while True loops
forever, or at least until something
within the loop causes it to exit.
def how_many_guesses(low=1, high=6):
""" Return number of guesses needed to guess a random number. """
import random
number = random.randint(low, high)
count = 0
while True: # always loop
count = count + 1
guess = int(input(f"Pick a number from {low} to {high}: "))
if guess == number: # Quick quiz: why '==' here, not '='?
return count # exit from both loop and function
else:
print("Nope; try again.")
result = how_many_guesses()
print(f"That took you {result} guesses")
Try that at pythontutor.com. (Copy that code and paste it in.)
Notice all the pieces that we've been talking about :
if statement with == comparisonOne last piece of syntax. This one is optional if your head is exploding already. (I know that we've been charging through this stuff quickly; in a 20-hour-per-week seven-week format, things are intense.)
When something goes wrong while a program is running, for example a division by zero or trying to convert 'cat' to an integer, the error that is created is called in python an "Exception". It's yet another kind of object, which will stop the program if it isn't handled in some way.
$ python
>>> a = 1/0 # runtime error : divide by zero
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ZeroDivisionError: division by zero
I'm sure that you've all seen these sort of things by now.
There is a way to contain errors like this so that they
don't halt the program. In python, that's done with a try
statement, which is a lot like an if. If an error happens,
the program jumps down to the except clause, which is
similar to an else .
The errors themselves are objects, with their own types
and methods. The except line can specific which sorts
of errors it can handle, and give a name to the error
so that it can be displayed or examined.
The official documentation at docs.python.org/3/tutorial/errors.html can be found by googling for example "python try except".
Here's an example.
print('Starting program that has 1/0 in it')
try:
print('line before error') # This line works fine.
a = 1/0 # The 1/0 is an error ... doesn't finish.
print('line after error') # This line never happens.
except Exception as e:
print('--- handling the error ----') # The 1/0 error jumps to here.
print(' error type : ', type(e)) # Print the error's type.
print(' error message : ', e) # Print the error's message.
print('---')
print('The program is still running!')
Again, try this at pythontutor.com to see what happens.
That's all for now!