
-->
assignments
1. getting started
due Thu Feb 24
- Explore this course website. Read the syllabus and browse the resources.
- Please join the slack channel. You can find information about it in the left menu after you log in. Introduce yourself, and ask a question.
- Review and/or brush up on your skills in these topics using the sources in the resources page :
- creating a source code file *.py or *.c with a code editor.
- running python or C from a unix commannd line shell prompt.
- In particular, you can review python basics with chapter 1 in runestone's pythonds. (This should be mostly review from Intro CS.)
- Submit a response to this assignment describe your computing and programming background, and what you hope to get out of this course. What sort of computer do you have - Mac? Windows? Unix?
- In Python, find all Pythagorean Triples with \( a \lt b \lt c \le N \) and
a + b + c = N for N = 1000. Hint: I suggest using the "brute force" approach. Please try this before Monday's class so that we can discuss it then. (For example, if I said N=12, you should find one triple, (a,b,c) = (3,4,5)).
- Can your program solve the problem for N = 10000? 100000? 1000000? How long does it take to run those? What is the largest practical value of N?
- Optional: repeat that Pythagorean search in the C programming language. Again, how long does it take, and how large a value of N can your code handle?
- Describe a sorting algorithm of your own invention, which will put a list of integers for example [10, 2, 1, 7] into the correct order e.g. [1, 2, 7, 10]. One way to think about this is to explain exactly what you would do if you were given a hand of 4 cards and asked to put them into into the correct order. There are many, many ways to do this, and we'll look at some of them over the next few weeks. At this point see what you can do with this with what you already know. (We'll mention a few ideas in class on Monday).
- Translate your sorting algorithm into python, put it into this sorting_template.py, and run it.
- Do submit your source code and results here, as attached files or embedded code, along with a discussion of what you did.
- Let me know how all this went : easy? hard?
2. analysis
due Thu Mar 3
- Read about algorithm analysis and O() notation. Some sources include
- Do some numerical experiments with randomly generated data of different sizes N to estimate the O(?) behavior of some of the following Python operations. To estimate the timing of very fast operations, repeat the operation a large number of times. Or use the python timeit package. Try to time just the operation you're interested in, not setting things up. Make at least one plot to visualize one of the results.
- (x in y) where y is a list
- (x in y) where y is a set
- (x.sort()) where x is a list (hint: you should get behavior slower than O(n) but faster than O(n*n).)
- Say you have an algorithm with O() behavior described by one of these four functions ( N log(N) , \(N^2\) , \(2^N\) , N! ) . For each, what values of N do you think it would be practical to run a program with that behavior? Would N=10000=1e4 be practical? N=1e6? Make a plot of N vs time that illustrates what's going on.
- A sorting algorithm takes 1 second to sort 1000 items. About how long do you think it take to do to 10,000 items if (a) the sorting algorithm is \( O(n^2) \) or (b) the sorting algorithms is \( O(n \, log(n)) \).
- Suppose you want search for a text string in a book sized document. Which is better, an O(1) algorithm or an O(n) algorithm? Discuss. (Hint: this is a trick question.)
3. linked lists
due Mon Mar 14
- Read about C pointers, structs, and malloc, and Python classes.
- Start reading about linked lists, stacks, and queues.
- All of the rest of these coding problems can be done in either Python, C, or both. For full credit, do at least some work in C.
- First, download, examine, and run my linked list code.
- Add a
find(value) function which does a search to see if a given value in the list, returning True of False. Can you do this recursively? In a loop?
- Add a function to insert a value after a given value. This should start by first finding that value, then altering the linked list. What O() is this operation, and why? Can you do this for the IndexedArray ... without using python's built-in insert? What O() would that be, and why?
- Here's a new algorithm problem to try. First try it on your own, but if you need to you can read about this problem in the Runestone pythonds, 4.6 and following.
- Write a function to return True or False depending on whether a string made up of "(" and ")" has all the parens matching. For example, "(())" is True, while "((" is False.
- Expand your function to include parens, brackets, and braces, for example "({})" is True, while "({)}" is False. (Hint: a stack can help ...)
4. sorting
due Mon Mar 21
- Read about sorting algorithms - Skienna's book or the runestone python online book are some reasonable choices.
- In either python or C, implement and test a function that reverses a singly linked list. Your code should run in O(n) time. (This is a classic linked-list exercise, all about rearranging pointers.)
- Implement either BubbleSort or QuickSort in python or C, run on a test case, and explain what its
O() behavior is and why.
- Explain what a "loop invariant" is, and why they can be helpful in showing that an algorithm is valid. See for example wikipedia and this discussion of bubble sort. How is this connected to "proof by induction"?
- Choose a sorting algorithm that we haven't discussed to start studying for your midterm project, and tell me which one you're going to look at. (MergeSort is a good choice if you're not sure ... which can be done linked lists in place!) Where are you reading about it?
5. midterm project
due Thu Mar 31
- This is for one of your three semester grades.
- With a sorting algorithm that we haven't done in class (mergesort is a good choice), implement, explain, discuss the expected
O() behavior of, and perform numerical experiments to show that behavior on lists of random numbers of various sizes. You can use either timing or number of steps as a measure.
- You may use either Python or C, or for extra brownie points both. (In C, I'd suggest outputting the results to a text file, and plotting those numbers in a python or R notebook.)
- Think of this as a short paper - I want to see an explanation, code, output from the code, some graphs, references of what sources you used - all that.
6. hash tables
due Mon Apr 11
- Read about hash tables - what they are and how to implement them. There are several sources in my notes from last week.
- Implement and test a hash table, in either C or Python, doing something like the examples in the code/hash_tables folder. Use a different hash function, a different collision mechanism, try different sizes for the hash tables - any variation is fine. The point is to play around with and understand how these things work. Do include some sort of tests for your code to see how well it works. All the specifics are up to you.
- In theory, hash tables give us fast O(1) lookup for (key, value) pairs. In practice, collisions may slow this down if we aren't careful. Explain what this means practically for your hash table code.
7. graphs
due Mon Apr 18
- Consider this graph :
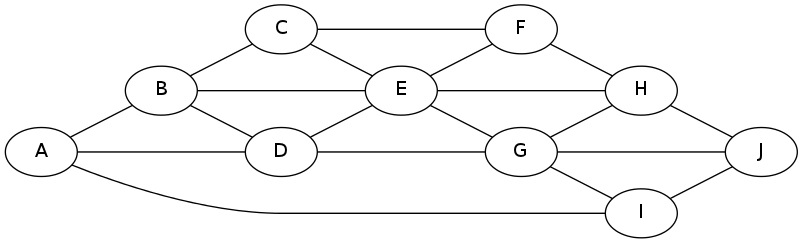
- What kind of graph is this? (In other words, what are its properties?)
- Put into code both (a) an "adjacency matrix" and (b) an "adjacency list" representation of the graph.
- Run both a depth-first and breadth-first traversal starting at A, find the order that the nodes are visited for each, and explain why you get that result and what's going on.
- Explore at least one of the example python programs that showed this week for some classic problems. Study the code, run some of it with some of your own debugging print statements, perhaps put it into pythontutor. Show your understanding by explaining what it's doing and how it works.
8. shortest path
due Mon Apr 25
- Read about and explain four classic algorithms for two classic graph problems, as described in my notes.
- What exactly is the "shortest path" problem?
- Summarize the basic ideas behind (a) Dijkstra's algorithm and (b) the Floyd-Warshall algorithm.
- For at least one of those two, work through the algorithm step by step by hand on a tiny example of your choice. Include and explain whatever data structures are needed.
- You may want to use my code to check your "by hand" result.
- What exactly is the "minimum spanning tree" problem?
- Summarize the basic ideas behind (a) Prim's algorithm and (b) Kruskal's algorithm.
- For at least one of those two, work through a tiny example by hand step by step, including any needed data structures.
- You may use my code to check your work, but I'm looking for an explanation more than running code.
- Start thinking about what you might want to do for a final project - a problem, algorithm to solve it, code to implement it, a discussion and analysis. Tell me what you're thinking of doing.
9. SQL
due Mon May 2
- Tell me what you want to do for a final project, what resources you've found to learn about it, and start reading up on it.
- Explore some of the SQL exercises on the resources page such as those at swcarpentry. (I worked through how to get going with sqlite3 in a terminal on jupyter.bennington.college in our Thursday May 28 zoom class). Describe what you did, with some specific examples. Also :
- Explain what a "JOIN" is and give an example.
- How does that compare with a "SELECT" within another "SELECT" ?
- Explain what a "B-tree" is, what it has to do with SQL, and what it's O() behavior is for its basic API operations.
10. complexity
due Thu May 12
- Work on your final projects.
- Browse through my complexity notes and come to class ready to discuss.
- Explain your understanding of P vs NP - what that all about and why does it matter.
- optional: read about and practice regular expressions.
- optional: use my finite state simulator to create a machine which accepts strings made up of 0's and 1's where the number of 1's is a multiple of three.
11. draft of final project
due Mon May 16
- Please turn in a draft of your final project!
12. final project
due Mon May 23
- Come to class on Monday ready to share your project.
- Turn in the paper, code, pictures, bibliography and all that by Thursday.
13. semester evaluation
due Mon Jun 6
- A place for the term grade.

